[latexpage]
Al finalizar el estudio de este tema, el estudiante de Matemática intermedia 1, estará en capacidad de calcular integrales que contienen potencias de funciones trigonométricas. En algunos casos puede ser necesario utilizar las técnicas de integración de las secciones anteriores.
Documento del tema
2.2 Integrales trigonométricas
Sugerencias para este tema
- Si la integral contiene una potencia impar de senos y cosenos, descomponga la potencia impar en una potencia par y el diferencial. Utilice una identidad para trasladar la potencia par a la otra función y haga una sustitución.
- Si la integral contiene solo potencias pares de senos y cosenos, utilice las fórmulas de reducción de potencias.
- Si la integral contiene solo potencias de tangentes y secantes y la secante tiene potencia par. Descomponga la potencia de la secante en dos partes, con una de ellas obtenga el diferencial y la otra parte se convierte a tangentes utilizando una identidad y haga una sustitución.
- Si la integral contiene solo potencias de tangentes y secantes y la tangente tiene potencia impar. Reduzca una potencia a la tangente y una a la secante para obtener el diferencial de la secante convierta la potencia par de tangente a secantes utilizando una identidad y haga una sustitución.
- En otros casos puede utilizar integración por partes, otras identidades trigonométricas o alguna sustitución.
Problema resuelto 1

Problema resuelto 2

Problema resuelto 3
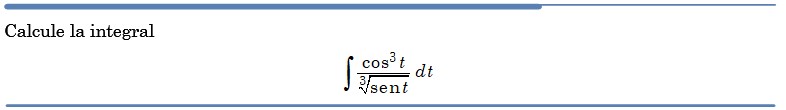
Problema resuelto 4
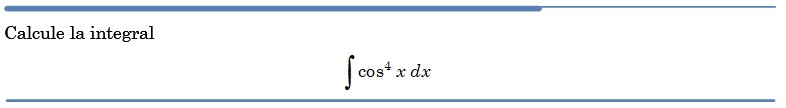
Problema resuelto 5

Problema resuelto 6

Problema resuelto 7
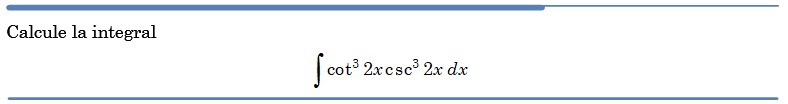
Problema resuelto 8
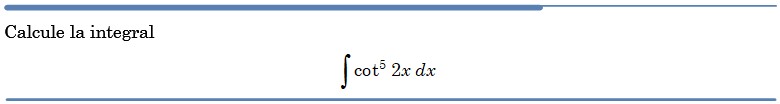
Problema resuelto 9

