[latexpage]
El teorema fundamental del cálculo relaciona el cálculo diferencial con el cálculo integral. Este teorema consta de dos partes
Parte 1:
Si una función $f$ es continua en el intervalo cerrado $[a,b]$ y $F$ es una antiderivada de $f$ sobre ese intervalo, entonces
\[ \int_{a}^{b}f(x)dx=F(b)-F(a) \]
Parte 2:
Si $f$ es una función continua en el intervalo cerrado $[a,b]$ y $x$ es cualquier número en el intervalo, entonces
\[ \frac{d}{dx}\left [ \int_{a}^{x}f(t)dt \right ]=f(x) \]
Sugerencias para este tema
- Para calcular una integral definida primero calcule la antiderivada F(x)
- Después de calcular la antiderivada, evalúe F(b) – F(a).
- Si al calcular la antiderivada, se hace alguna sustitución. Se pueden cambiar los límites de integración en términos de la nueva variable y evaluar la integral en términos de la nueva variable.
- La parte 2 del teorema fundamental es valida solamente si el límite inferior es una constante y el límite superior es x. En cualquier otro caso será necesario realizar una sustitución y utilizar la regla de la cadena.
Problema resuelto 1
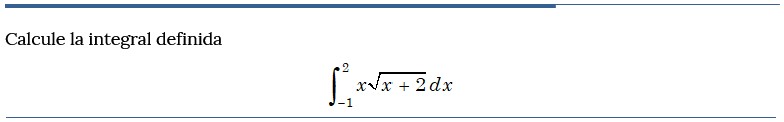
Problema resuelto 2
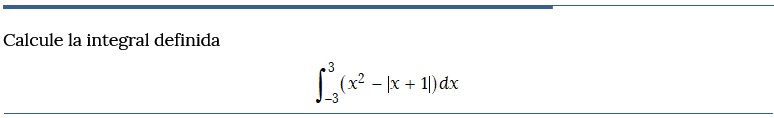
Problema resuelto 3

Problema resuelto 4

