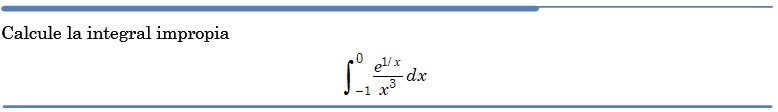[latexpage]
Al finalizar el estudio de este tema, el estudiante de Matemática intermedia 1, estará en capacidad de calcular integrales impropias cuando uno de los límites de integración es infinito e integrales impropias cuando la función no está definida en uno de los límites de integración.
Documento del tema
Sugerencias para este tema
- Para calcular una integral impropia con un límite de integración infinito, sustituya el infinito por una constante, Evalúe la integral en términos de la constante y luego calcule el límite cuando la constante tiende al infinito.
- para calcular una integral impropia, cuando la función a integrar no está definida en uno de los límites de integración, sustituya el valor donde la integral no está definida por una constante, evalúe la integral en términos de la constante y luego calcule el límite cuando la constante se aproxima al número por la derecha o por la izquierda según corresponda.
- Es importante observar que la función a integrar esté definida para todos los valores entre los límites de integración, si éste no fuera el caso será necesario dividir la integral en dos o más integrales impropias.
Problema resuelto 1
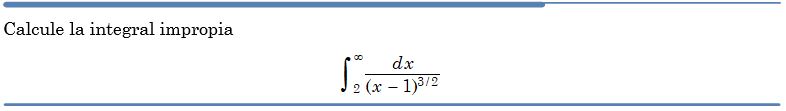
Problema resuelto 2
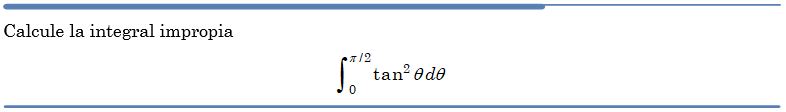
Problema resuelto 3
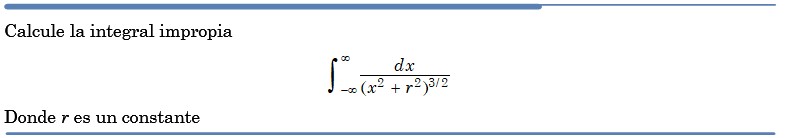
Problema resuelto 4