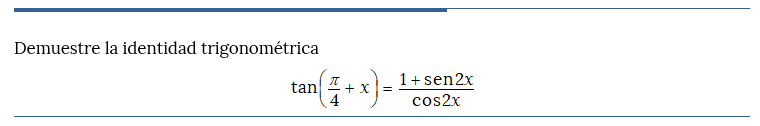[latexpage]
Sugerencias para demostrar identidades trigonométricas
- Al demostrar una identidad, se debe elegir uno de los lados y por medio de operaciones algebraicas y sustituciones trigonométricas demostrar que es igual al otro lado.
- Si uno de los lados de la identidad es más complejo que el otro, generalmente es mejor probar con éste lado, hasta demostrar que es idéntico al otro lado.
- Si en el lado elegido se pueden realizar operaciones algebraicas como suma de fracciones, factorizaciones, desarrollo de binomios; desarrolle éstas operaciones.
- Cuando no se puedan realizar operaciones algebraicas utilice las identidades para efectuar alguna sustitución y realice de nuevo las operaciones algebraicas resultantes. No pierda de vista el otro lado, pues las operaciones realizadas deben conducir a obtener esa expresión.
- Una alternativa que funciona con mucha frecuencia consiste en expresar uno de los lados en términos de senos y cosenos, y luego efectuar las operaciones algebraicas resultantes.
- En algunas identidades no hay operaciones algebraicas por realizar ni sustituciones trigonométricas por hacer. En estos casos suele ser útil multiplicar el numerador y el denominador por el conjugado del denominador, lo cual permite realizar operaciones algebraicas.
- Para demostrar una identidad que contiene sumas o múltiplos de ángulos, se sugiere utilizar la identidad correspondiente y trabajar con el lado que contiene sumas de ángulos o ángulos múltiples.
- Las identidades trigonométricas fundamentales y algunas otras identidades útiles son


Documentos sobre el tema
Problema resuelto 1
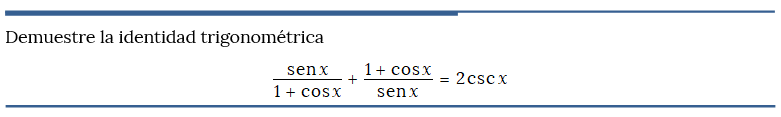
Problema resuelto 2

Problema resuelto 2
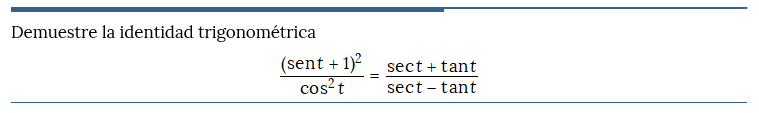
Problema resuelto 4