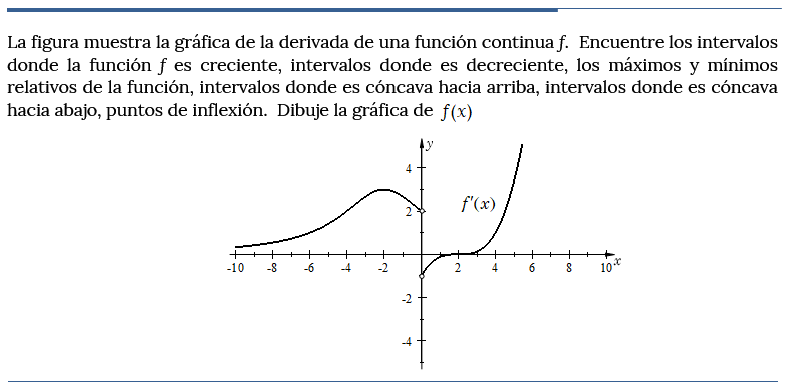
[latexpage]
En esta sección se estudia trazo de gráficas de funciones utilizando calculo diferencial, utilizando la primera y la segunda derivada de la función.
Sugerencias para el trazo de gráficas
- Calcule la primera y la segunda derivada de la función.
- Determine los números críticos, en los cuales la primera derivada es igual a cero y los números donde la primera derivada no está definida.
- Determine los números donde la segunda derivada es igual a cero y los números donde la segunda derivada no está definida.
- Con los valores obtenidos en los incisos anteriores construya los intervalos en donde realizará el análisis de la función.
- Para cada intervalo determine si la función es creciente o decreciente evaluando un número del intervalo en la primera derivada. Determine si la función es cóncava hacia arriba o hacia abajo evaluando el mismo valor en la segunda derivada.
- Con el análisis de los intervalos anterior y posterior a cada número crítico, determine si en el valor crítico hay un máximo relativo, un mínimo relativo, o un punto de inflexión. Utilice para ello los criterios de primera derivada, segunda derivada y el del punto de inflexión.
- Para dibujar la gráfica primero localice los puntos correspondientes a máximos, mínimos y puntos de inflexión, luego dibuje los arcos de curva correspondientes a cada intervalo según los resultados contenidos en la tabla construida anteriormente.
Documentos sobre el tema
Problema resuelto 1

Problema resuelto 2

Problema resuelto 3

Problema resuelto 4

Problema resuelto 5