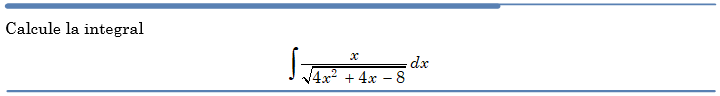[latexpage]
Al finalizar el estudio de este tema, el estudiante de Matemática intermedia 1, estará en capacidad de calcular integrales que contienen expresiones de la forma
1. $ a^2-u^2 $ 2. $ a^2+u^2 $ 3. $ u^2-a^2$
Estas expresiones generalmente estarán en el numerador o denominador de una fracción con un exponente fraccionario.
Documento del tema
2.3 Sustitución trigonométrica
Sugerencias para este tema
- Si la integral contiene la expresión 1, la sustitución trigonométrica es $u=a\sin \theta $. Se recomienda construir un triángulo rectángulo con hipotenusa «a» y cateto opuesto «u».
- Si la integral contiene la expresión 2, la sustitución trigonométrica es $u=a\tan \theta $. Se recomienda construir un triángulo rectángulo con cateto adyacente «a» y cateto opuesto «u».
- Si la integral contiene la expresión 3, la sustitución trigonométrica es $u=a\sec \theta $. Se recomienda construir un triángulo rectángulo con hipotenusa «u» y cateto adyacente «a».
- Una vez realizadas las sustituciones en la expresión a integrar y del diferencial , calcule la integral que contiene funciones trigonométricas.
- Cuando se ha terminado de calcular la integral no olvide expresar la respuesta en términos de la variable «x», para ello se puede apoyar nuevamente en el triángulo rectángulo.
Problema resuelto 1
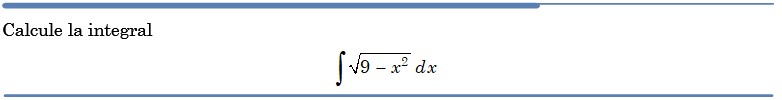
Problema resuelto 2
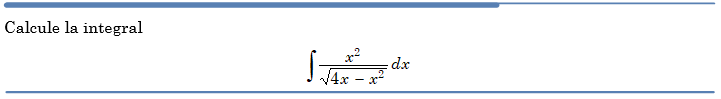
Problema resuelto 3
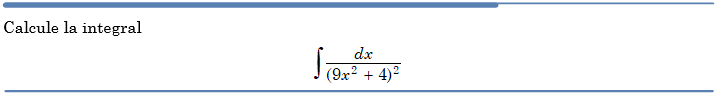
Problema resuelto 4
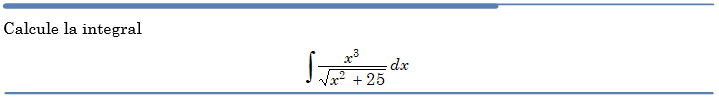
Problema resuelto 5
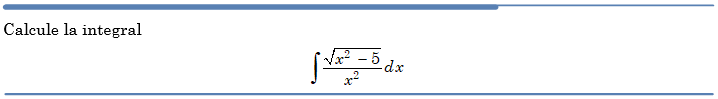
Problema resuelto 6