[latexpage]
En esta sección se estudia el cálculo de límites utilizando la regla de L’hopital. Utilizando este teorema se pueden calcular límites que de otra manera es prácticamente imposible hacerlo.
Sugerencias para calcular límites usando la regla de L’Hopital
- Si el límite tiene forma indeterminada $\frac{0}{0}$ o bien forma indeterminada $\frac{\pm \infty }{\pm\infty}$. Calcule la derivada del denominador y la derivada del denominador y evalúe nuevamente el límite. Si el resultado es un número real, ese es el límite. Si obtiene de nuevo una forma indeterminada, repita de nuevo este procedimiento.
- Si el límite tiene forma indeterminada $ \infty – \infty$. Manipule algebráicamente la función hasta obtener una de las formas indeterminadas $\frac{0}{0}$ o bien $\frac{\pm \infty }{\pm\infty}$.
- Si el límite tiene forma indeterminada $0\cdot \infty$, utilice la ley de extremos y de medios del álgebra para obtener una de las formas indeterminadas $\frac{0}{0}$ o bien $\frac{\pm \infty }{\pm\infty}$.
- Si el límite tiene una de las formas indeterminadas $ 0^{0}, \infty^{0}, 1^{\infty} $, utilice logaritmos naturales para trasladarlo a la forma $0\cdot \infty$. Calcule el límite siguiendo el procedimiento del inciso anterior. Finalmente aplique la función exponencial natural para obtener la respuesta.
Problema resuelto 1
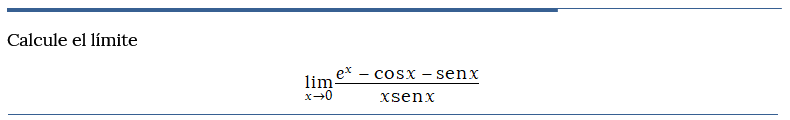
Problema resuelto 2

Problema resuelto 3

Problema resuelto 4

Problema resuelto 5

Problema resuelto 6

