[latexpage]
Área bajo una curva
Si una función $f$ es continua en el intervalo cerrado $[a,b]$ y la función es mayor o igual a cero en dicho intervalo. El área bajo la curva se puede aproximar utilizando la suma de Riemann
\[ A\approx \sum_{i=1}^{n}f(c_{i})\Delta x \]
El valor exacto del área bajo la curva está dado por
\[ A=\lim_{n\rightarrow \infty }\sum_{i=1}^{n}f(c_{i})\Delta x \]
La integral definida
Si $f$ es una función definida en el intervalo cerrado $[a,b]$. Entonces la integral definida de $f$ de $a$ a $b$, está dada por
\[ \int_{a}^{b}f(x)dx=\lim_{\left | \Delta \right |\rightarrow 0}\sum_{i=1}^{n}f(c_{i})\Delta x_{i} \]
Documentos del tema
Sugerencias para este tema
- Para calcular en forma aproximada el área bajo una curva en un intervalo cerrado, utilice una suma de Riemann para un número dado n. Si no le indican otra cosa utilice el extremo derecho.
- Para calcular el área exacta bajo una curva (para ciertas funciones) utilice el límite cuando n tiende al infinito de una suma de Riemann. Si no le indican otra cosa, utilice el extremo derecho.
- Algunas integrales definidas se pueden calcular interpretándolas en términos de áreas de figuras geométricas.
Problema resuelto 1

Problema resuelto 2
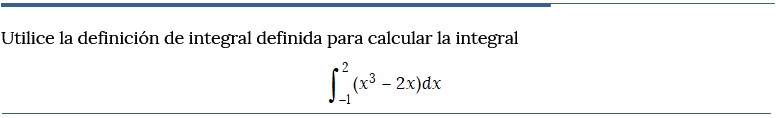
Problema resuelto 3
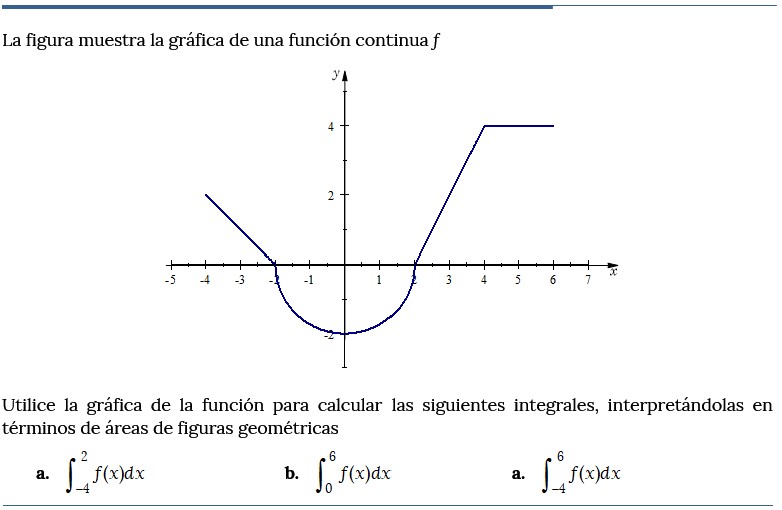
Problema resuelto 4

