[latexpage]
Cuando se calcula un límite de la forma
$latex \displaystyle \underset{{x\to c}}{\overset{}{\mathop{{\lim }}}}\,\frac{{f(x)}}{{g(x)}}$
y se obtiene que el límite del numerador $latex \underset{{x\to c}}{\overset{}{\mathop{{\lim }}}}\,f(x)=k$ y que el límite del denominador $latex \underset{{x\to c}}{\overset{}{\mathop{{\lim }}}}\,g(x)=0$, donde $k$ es un número diferente de cero; se dice que el límite es infinito. En estos casos el límite no existe ya que la función crece o decrece sin límite tomando valores positivos o negativos muy grandes.
La recta $x=c$ se llama asíntota vertical.
Sugerencias para para calcular límites infinitos
-
- Calcule el límite cuando $x$ se aproxima a $c$ por la derecha, para hacerlo de forma sencilla evalúe la función en un valor ligeramente mayor que $c$. Si el resultado es positivo el límite es infinito positivo, si el resultado es negativo el límite es infinito negativo.
- Calcule el límite cuando $x$ se aproxima a $c$ por la izquierda, para hacerlo de forma sencilla evalúe la función en un valor ligeramente menor que $c$. Si el resultado es positivo el límite es infinito positivo, si el resultado es negativo el límite es infinito negativo.
- Si el límite por la izquierda y el límite por la derecha de $c$ son ambos infinito positivo, se concluye que el límite es infinito positivo.
- Si el límite por la izquierda y el límite por la derecha de $c$ son ambos infinito negativo, se concluye que el límite es infinito negativo.
- Si el límite por la izquierda y el límite por la derecha de $c$ son distintos, se concluye que el límite no existe.
Problema resuelto 1
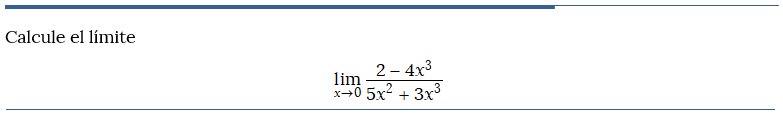
Problema resuelto 2
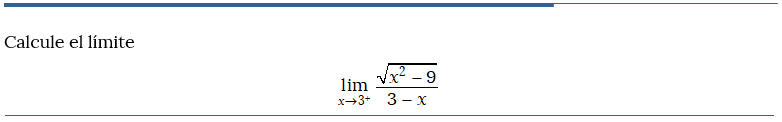
Problema resuelto 3
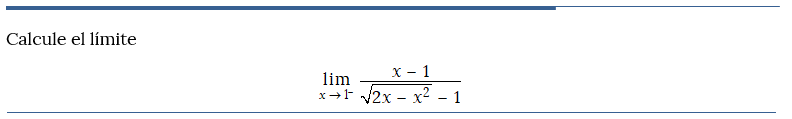
Problema resuelto 4
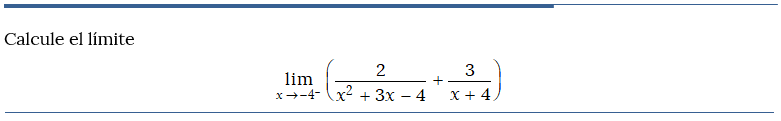

🙂 Muy util