[latexpage]
En esta sección se estudian los limites al infinito. Estos límites permiten estudiar el comportamiento de las funciones cuando el valor de x se aproxima al infinito positivo o bien cuando el valor de x se aproxima al infinito negativo
Resumen de contenidos
Sugerencias para calcular límites al infinito
-
- Si el límite tiene una de las formas indeterminadas $ \frac{\infty}{\infty}$, multiplique el numerador y el denominador por un factor $ \frac{1}{x^r}$, en donde $r$ se sugiere que se tome como el grado del denominador.
- Si el límite tiene forma indeterminada $\infty -\infty$, se sugiere simplificar la expresión algebraica si este fuera el caso y luego utilizar el teorema de límites al infinito.
- Si la expresión contiene una suma o diferencia de radicales se sugiera racionalizar la expresión multiplicando por el conjugado, para obtener una expresión racional y poder así utilizar los teoremas de límites al infinito.
- Si la función es una función compuesta se debe utilizar el teorema del límite de una función compuesta.
Problema resuelto 1
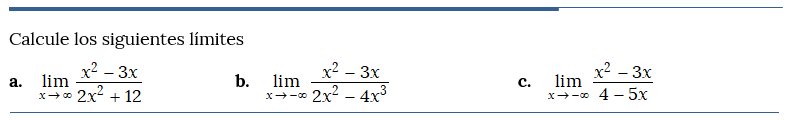
Problema resuelto 2
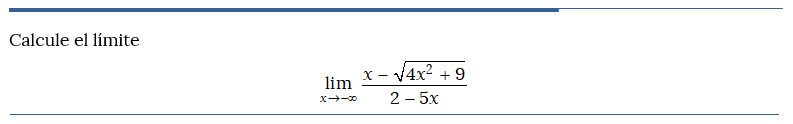
Problema resuelto 3
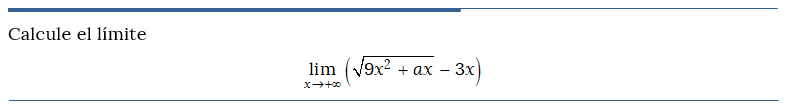
Problema resuelto 4
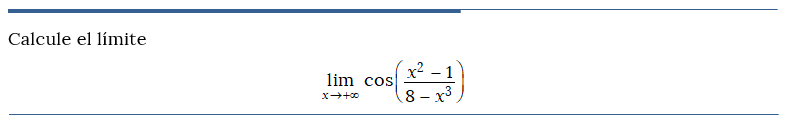
Problema resuelto 5

